July Summer Immersion 2019: Introduction to the Logic of Set Theory

July 2019 SUMMER IMMERSION - Introduction to Logic of Set Theory

What is a Summer Immersion?

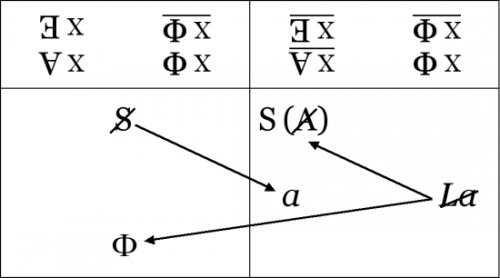
The Summer Immersion of PLACE is a course, and unlike a seminar or cartel, it has as its goal an instruction into problems of reading and writing that are most often reserved for technical expositions in the sciences and mathematics. It is an intensive once a week meeting for 5 weeks designed to transmit a technical writing in a non-technical and un-coded way. Many working in the field of analysis have little familiarity with this method of writing and, therefore, bypass its effectivity for a practice of ignorance and verbalism. Indeed, for over thirty years many have written on Lacan’s formulas of sexuation by giving the diagram in predicate logic above a delirious reading. Without denying a delirium to anyone, the goal of the Summer Immersion is to present this logic in a more precise way and in a manner closer to the work of Lacan.

To do so, our course aims to provide the background for a purely constructive approach to the theory of sexuation in the logic of predicates and set theory. We take as a premise there is no lacanian topology, logic, set theory, etc., or if there is, it is without interest. What is crucial, however, are problems of set theory and logic opened up by Lacan in the field of analysis that have a direct import not only for mathematical logic, but for the clinic.

Admission: Open to anyone without any prior background in lacanian analysis, set theory, or logic .

Date: Beginning at Saturday July 6^th,from 10:00am to 12:30pm it meets every Saturday concluding on  Aug.3 for a total of five seances.

Economy: The tuition is $400.

Participation: in person and by Skype is available to those outside the vicinity of Los Angeles.

Instructor: Tate-Robert Groome

Registration: Contact the secretary at PLACE@topoi.net

Course Description: Introduction to Logic of Set Theory

We begin with a stacking of three separate languages:

1) Propositional Logic

2) Predicate Logic

3) Set Theory

that the participant is introduced to both in the course and through outside readings (see the reading list at the end of the course description). Before one can do anything more than merely comment on and mimic a practice of the formulas of sexuation, one should stake out a practice of at least these three languages.

To begin to work in these theories-languages we will determine the following.

1) A definition of Logic as The Necessary Writing of A Discourse (Lacan): a non-psychological and non-normative definition that does not fall back into the notions of logic as ‘The Laws of Thought’ (Boole) or ‘The Laws of Necessary Thought” (Frege). If Logic is most often correlated to a theory of necessity and deduction, it will be important not to conflate it with Mathematical Logic since the latter introduces problems of contingency and construction that are closer to problems of geometry, than logic. By not avoiding problems of construction that arise in Mathematical Logic problems of contingency can be shown to be relevant to Logic itself. Thus, resolving in advance a common bypass of Logic in the appeal to deviant, alternative, or philosophical logics. The questions are no longer there: it is never a question of opposing a rigid conception of logic to alternative logics, but the problem of the contingency posed by a mathematical construction of the necessity of a logical deduction. For our introduction builds on a table that may very well be given as an abbreviation of the tradition of Mathematical Logic itself:

One way to read this table is to ask whether everything in a theory has a name, if so, then our theory is complete and we are working in first-order predicate logic and propositional logic; a logic of deduction and derivation, respectively. If not, then our theory is incomplete and we are working in set theory, i.e., a theory rich enough to introduce mathematics and the paradoxes of Russell and Cantor. To introduce the participant to this work, we will concentrate on providing the framework for a theory of predicates, in particular the theory of quantification, in correlation with both a theory of logical deduction/derivation and logical nomination/description (Hintikka, Lacan).

2) A definition of Set: by defining a Set naively, as a One that it is Many (Cantor), paradoxes arose such as Russell’s (the set of sets not a member of itself) and Cantor’s (the set of all sets) that threatened the determination of what exactly One-set is. Then came Zermelo who showed how to not only save set theory through an axiomatization determining what One-set is, but opened up a whole new field of Non-Sets or Class theories in the manner of Bernays/Gödel/ Von Neumann. Yet, before  one could determine a theory of Non-sets or Classes, there was a previous question raised by Hilbert, then Bourbaki, as to what constitutes the Name of a Set or what would later be called an Assembly (Hilbert/Bourbaki).  Schematically, this movement can be formulated as:

The movement from Set —> Class —> Assembly and, respectively, One –> Non –> Name will first be introduced in a reference to Zermelo axioms  (ZF), then in a construction of a formalized language and model in the method of Bourbaki and Krivine.

This introduction will consist, practically, on introducing a simple method for both diagramming the axioms of Zermelo’s set theory in Euler-Venn diagrams and determining a decision procedure in a matrix/truth table. With these simple constructions at hand, we will proceed to give our first demonstrations in a mathematical logic, then return to show how the formulas of sexuation first brought out by Lacan are nothing other than a logic of set theory.

The course will conclude around two methodological resolutions:

1) by reducing the naive and axiomatic determinations to a set defined in terms of an  Assembly and a formalized language, we will have effectively replaced any need for a hypothesis on the philosopher’s L'Être et Evénement (Being and Event) with Lettre et Signifiant.

2) Lacan’s formulas of sexuation will have been effectively put into correspondence with the mathematico-logical tradition and not left as an excuse to improvise a delirium. In short, if there is a ‘beyond’ tradition pertaining to Lacan’s work in logic and mathematics it is not in the anarchic sense, but in the sense it advances the work of not only the psychoanalysts, but the mathematicians and logicians themselves.

T.R.Groome

Santa Monica

SUMMER 2019

=====================================================================

Reading Material of the Course:

1) Quine’s Methods of Logic and The Logic of Set Theory

2) Church’s Mathematical Logic

3) Bourbaki’s Theory of Sets (English Translation)

4) Zermelo’s original 1908 article Investigations in the Foundations of Set Theory (English Translation)

5) Frankel’s Foundations of Set Theory and Abstract Set Theory

Books and references may be found on the website and virtual website of PLACE.

If there are any questions on the course, materials, or modality of participation, please contact the secretary of PLACE at; PLACE@topoi.net